No more secrets Part 7:A computer must be able to compute!
We have seen circuits that can be used to select or route signals.
The main function of a computer is (obviously) to perform computations. The basic computation is the sum.
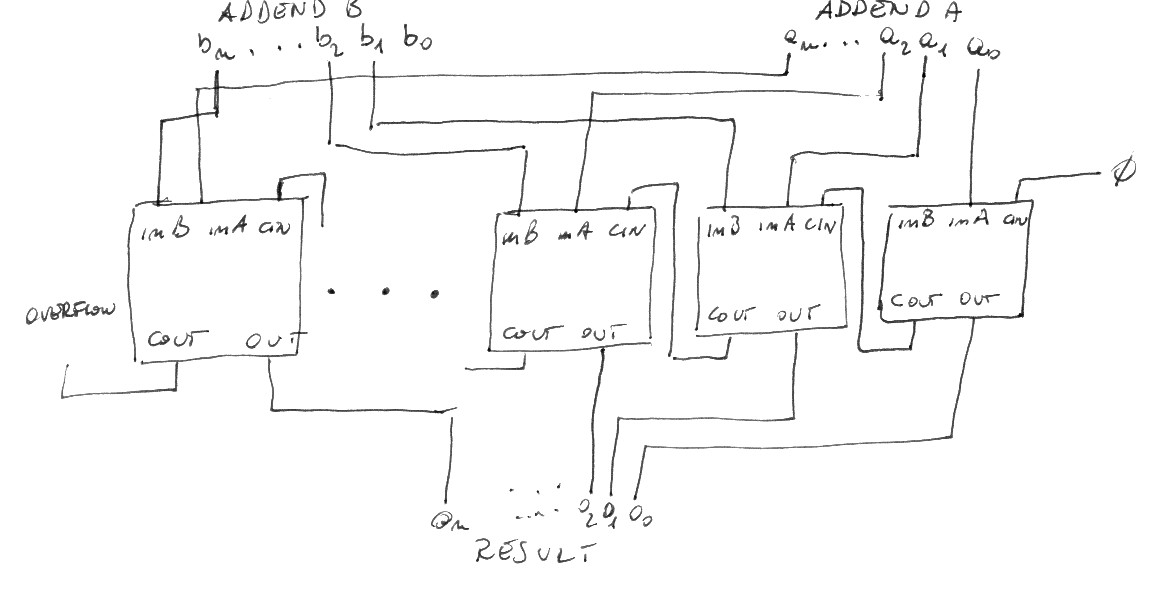
We are going to implement a full adder: a circuit that sums three bits together and provides two output bits, result and carry. In fact, to add two numbers having an arbitrary number of digits we need an algorithm to add three digits together. If you remember the algorithm to sum two numbers learnt in the elementary school, the sum must proceed column by column, right to left, in each column you have to add the two digits of both numbers plus the carry resulted in the computation of the previous column. You'll get two results in each column: the digit of the result and the new carry to be used in the computation of the following column.
inA inB Cin Cout Out 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1
From a closer look of the table it appears that the output is the count of the number of bits set to one in the input, encoded in binary. When the inputs are all zero the output is 00, all the configurations where there is only one bit set to 1 in the input (001, 010, 100) the output is 01, if two bits are one (011, 101, 110) the output is 10 and finally when all the input bits are set, the output is 11.
The most significant bit of the result has been named Cout, carry out as it has to be connected to the Cin input of another full adder in order to build a chain of adders able to sum an arbirary number of bits.
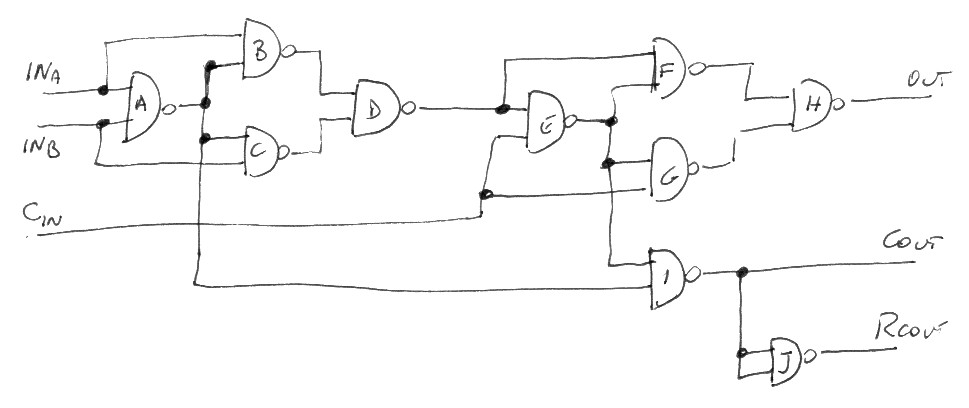
We need 9 NAND gates to implement a full adder on out breadboard.
This is the table of the jumpers
inA: AB inB: AC Cin: EG A: BCI B: D C: D D: EF E: FGI F: H G: H H: out I: JJ Cout J: Rcout
(Rcout is not currently used. It will be later used to implement the circuit of an entire ALU)
It is interesting to see how a simple circuit can compute a sum of three bits.
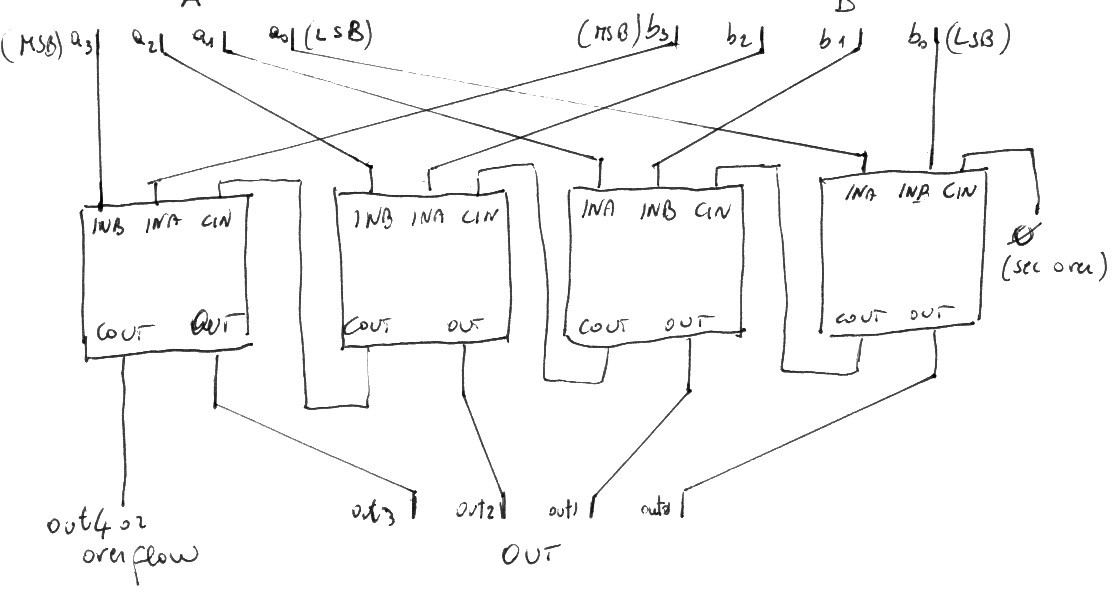
Several full adder bradboards can be chained to sum binary numbers. Using three boards it is possible to sum numbers from 0 to seven, four boards permit to sum numbers in the range zero to fifteen.
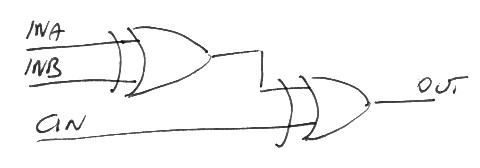
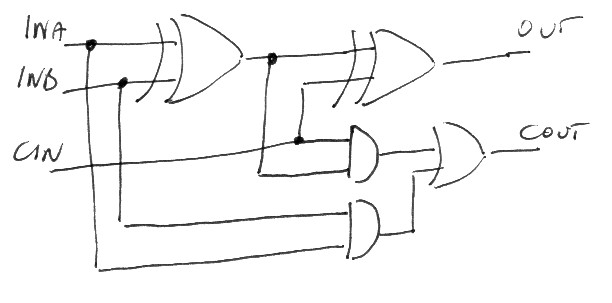
The circuit of the full adder uses two XOR gates to compute the result. In fact the result of the sum of two bits (not considering the carry bit) is a xor:
inX inY out 0 0 0 0 1 1 1 0 1 1 1 0 (and carry=1)
The circuit is implemented as two, two-bit adders in a pipeline.
For what concerns the carry, in the sum of two bits the carry is one when both inputs are one, thus it is the reault of an AND gate.
When the two two-bit adders are chaines in a pipeline to sum three bits at most one two-bit adder can generate a carry. The carry of the full adder is the result of an OR between the carry output of the two two-bit adders.
The full adder circuit implemented on the breadboard is the one depicted here above, implemented using only NAND gates.